Key Concepts
2d/3d - DeBroglie works for both 2d and 3d generation, by selecting an appropriate ITopology. Generally, most APIs accept (x,y,z) co-ordinates - the z value should just be 0 if you are working in 2d.
Tile - The individual units the generation algorithm works with. Tiles wrap a value of any type, but they are usually an integer index into a tileset, or a @System.Drawing.Color when working with bitmaps. The value isn't important, all relevant information about a tile is stored externally.
ITopology - Specifies an area or volume of space and how to navigate it. There's more detail in the topology section.
ITopoArray<T> - A 2d or 3d read-only array with one entry per space in the corresponding @DeBroglie.Topo.Topology. They are used as both the input and output format for the library. You can construct these with methods on TopoArray. ITopoArray objects can optionally have a mask associated with them, indicating missing values.
Model - A model specifies constraints between nearby tiles in the generated output. See models for more info.
Propagator - A propogator is responsible for generating an output that satifies the constraints specified by the model and other constraints.
Features
Models
Models are the key way to control the generation process in DeBroglie. They specify what combinations of tiles are legal to place near each other.
Models have only have a few parameters - most information is inferred by giving them samples tilemaps.
Adjacent
AdjacentModel constrains which tiles can be placed adjacent to which other ones. It does so by maintaining for each tile, a list of tiles that can be placed next to it in each direction. The list is always symmetric, i.e. if it is legal to place tile B directly above tile A, then it is legal to place A directly below B.
Adding a sample to an adjacent model adds all adjacent tile pairs in the sample into the legal adjacency lists. You can also directly specify adjacent tile pairs.
The adjacenct model is very "loose" - it doesn't constrain the choice of tiles as much as the overlapping model. This makes it a good choice when the relationship between tiles is very complex, or you are adding a lot other constraints directly.
Example

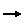

Overlapping
OverlappingModel constrains that every n by n rectangle in the output is a copy of a rectangle taken from the sample (potentially with rotation / reflection).
The model has three parametrs, nx, ny and nz which specify the dimensions of the rectangle/cuboid in the output. For convenience, you can just specify a value for n that sets all three. Typically n is only 2 or 3 - any larger and the algorithm can run quite slow and becomes increasingly unlikely to find a result. It also requires at least one sample - this model cannot be directly configured.
Compared to the adjacent model, the overlapping model is quite strict. This means it typically needs a larger amount of sample input to get good results, but when it does work, it can accurately reproduce many features of the samples that the adjacent model will simply scramble.
In particular, the overlapping model can detect corners, lines and junctions. In conjunction with the propogation by the Wave Function Collapse algorithm, this means that rooms and pathways will get detected and output, but with variations on the placement, size and direction.
Example

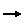


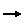

Other model functionaltiy
As mentioned, models also track the frequency of tiles in the sample image. You can make changes to this by calling MultiplyFrequency.

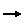



Constraints
Constraints are a way to make additional hard requirements about the generated output. Unlike models, constraints can be non-local, meaning they force some property of the entire image, not just within a small rectangles.
They are discussed on a separate page.
Backtracking
By default when you call Run() the WFC algorithm keeps adding tiles until it has filled every location, or until it is impossible to place a tile that satisfies all the constraints set up. It then returns Contradiction.
If you set the backtrack argument to true when constructing the TilePropagator, then the propagator does not give up when a contradiction occurs. It will attempt to roll back the most recent tile placement, and try another placment instead. In this manner, it can explore the entire space of possible tile placements, seeking one that satifies the constraints. Contradiction is only returned if all possibilities have been exhausted.
Backtracking is very powerful and general, and can solve extremely difficult layouts. However, it can be quite slow, and consumes a great deal of memory, so it is generally only appropriate for generating small arrays.
Topology
Topology is the abstraction DeBroglie to use to deal with 2d grids, 3d volumes and graphs under the same system. It is detailed here.
Rotation
Handling rotation of the input sample is a complex topic, and is discussed in a separate article.