Topologies
The most common case of using DeBroglie is to generate 2d images and tile maps, however, that is not all that can be generated.



DeBroglie uses a mechanism called ITopology to specify the type of area or volume to generate, what size it is, and whether it should wrap around at the edges (i.e. is it periodic). Topologies do not actually store data, they just specify the dimensions. Actual data is stored in an ITopoArray<T>, which associates a value with each cell of a given topology.
There are several types of topology supported:
- 2d square grid
- 2d hex grid
- 3d cube grid
- an arbitrary graph data structure
The grid ones are implemented with GridTopology, and graphs with GraphTopology. They share a common interface.
Each topology describes a set of cells (indexed consecutively from 0), how they correspond to 3d co-ordinates, and which cells are adjacent to each other, and in what direction. As WFC is a local algorithm, this is all the information needed for generation. However, some advanced features, such as mirroring, may not work with all topology types.
When using the command line tool, the topology is usually inferred from the input sample and does not need to be specified. But using the library, you will need to call an appropriate constructor, and pass the topology as an argument to various functions.
Square / Cube Topology
This is the most straightforward topology. It corresponds to a grid of cells, and the x,y,z co-ordinates correspond to the cartesian position in the grid. Almost all features support both of these topologies.
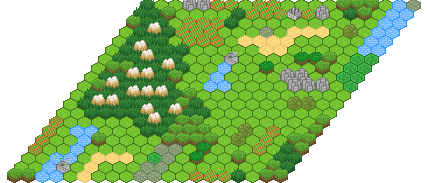
Hexagonal Topology
Hexagonal topologies use a convention of "pointy side up". The x-axis moves to the right, and the y-axis moves down and to the left. This means the library generates rhombus shaped output. Additionally, periodic input / output is not supported.
Using the Tiled format for import/export of hexagonal tilemaps is recommended, as most software doesn't have support for hexagons. DeBroglie comes with a separate library DeBroglie.Tiled to facilitate converting between ITopoArray<T> objects and Tiled maps.
When using the overlapping model, the constraints are based on n by n rhombus shapes, rather than n by n rectangles.
Graph Topology
Graph topologies have no special repeating structure, so require you to specify a complete list of neighbours for every cell manually. When converting to a co-ordinate, the x-axis corresponds directly to the cell index, and the other axes are unused.
Additionally, most models do not support the graph topology. You need to use the GraphAdjacentModel, which functions similarly to the normal AdjacentModel.
A MeshTopologyBuilder utility is provided to build graph topologies in the common case that the cells of the graph correspond to faces of the mesh.